문제
https://www.acmicpc.net/problem/9251
풀이
LCS(Longest Common Subsequence, 최장 공통 부분 수열)는 임의의 두 수열에서 각각의 부분 수열들 중, 서로 같은 부분 수열 중에서 가장 긴 수열을 의미한다.
문제의 예제를 보면 두 수열로 ACAYKP와 CAPCAK가 있다. 각 수열의 부분 수열은 아래와 같다.
- ACAYKP의 부분 수열 : {A}, {C}, {A}, {Y}, {K}, {P}, {A, C}, {A, A}, ... , {ACAYKP}
- CAPCAK의 부분 수열 : {C}, {A}, {P}, {C}, {A}, {K}, {C, A}, {C, P}, ... , {CAPCAK}
이들 중 {A}, {C}, {K}, {P}, {A, A}, ... , {A, C, A, K}와 같이 겹치는 부분 수열들이 있다. 이들 중 가장 긴 공통된 부분 수열을 구하는 문제이다.
해당 문제는 DP 문제로 Bottom-up 방식을 사용하여 풀었다.
탐색 중 같은 문자라면 이전 DP 값에서 +1을 해주고, 그 외의 경우는 행의 이전 값과 열의 이전 값 중 max() 값을 확인해서 값을 최신화하도록 했다.
두 수열 ACAYKP와 CAPCAK의 DP 값을 최신화하기 위해 아래의 좌측 표와 같이 그릴 수 있다.
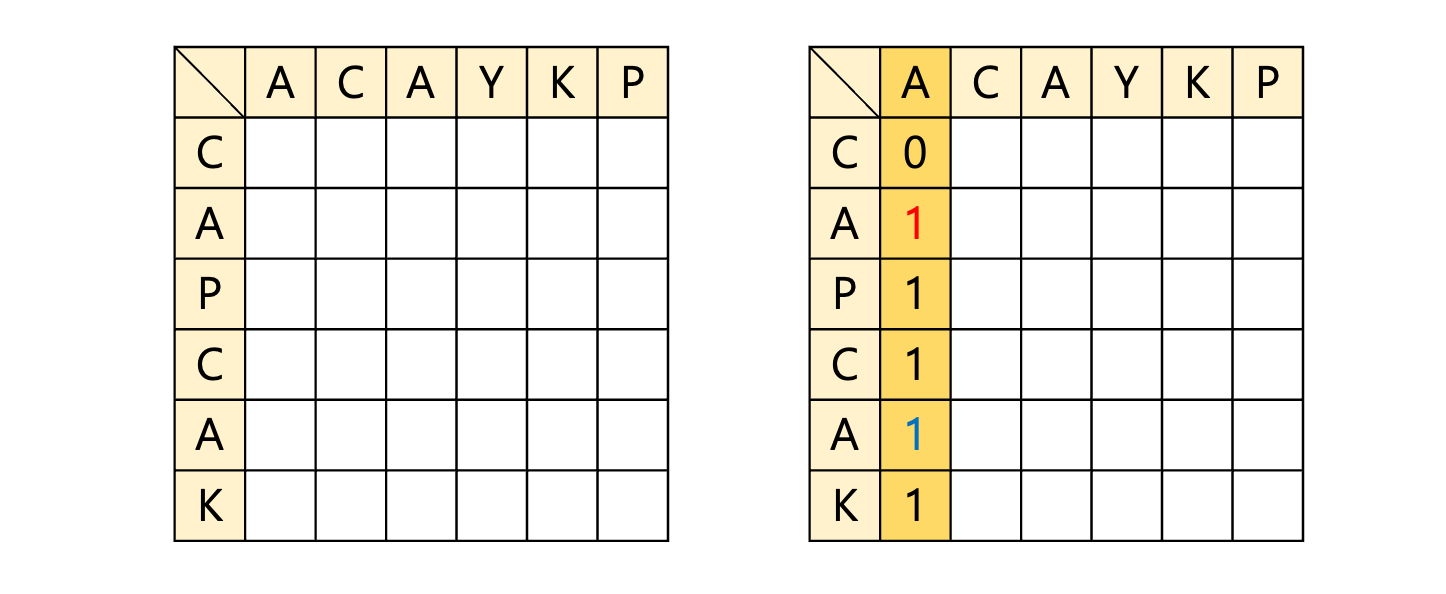
그리고 위의 우측 표를 보면 맨 앞 문자(A)부터 차례대로 비교하며 부분수열의 길이를 누적한다. ACAYKP의 첫 번재 문자인 A를 기준으로 CAPCAK의 문자들을 비교하면 위와 같이 값들이 표기된다.
빨간색으로 표기된 {A, A}에서 서로 같은 문자가 있으므로 +1이 되었다. 그런데 파란색으로 표기된 {A, A}에서도 서로 같은 문자지만 값이 1만큼 증가되지 않은 이유는 현재 ACAYKP의 첫 문자를 비교하고 있으며, {A}와 {C, A, P, C, A}의 최장 부분수열은 {A} 하나 뿐일 수 밖에 없기 때문이다.
이어서 다음 열을 채우겠다.
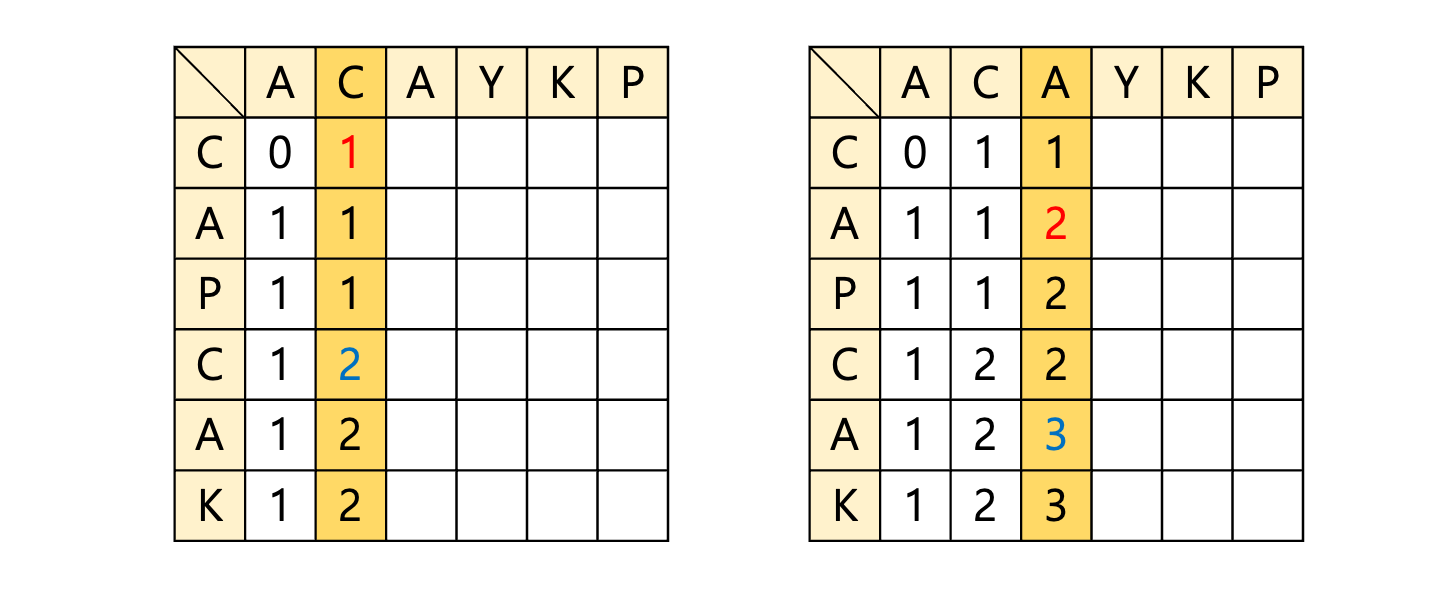
위의 좌측 표를 보면 빨간색 부분에서 {A, C}와 {C}의 부분수열은 {C} 이므로 +1이 되고, 파란색 부분에서 {A, C}와 {C, A, P, C}의 부분수열은 {A, C} 이므로 +1이 증가되어 2가 된다.
이어서 다음 열을 채우면 우측 표가 되며 {A, C, A}와 {C}의 부분수열은 {C} 이므로 +1이 되어 1이 되고, 빨간색 부분의 {A, C, A}와 {C, A}의 부분수열은 {C, A}가 되어 +1을 하여 2가 되고, 파란색 부분에서 {A, C, A}와 {C, A, P, C, A}의 부분수열이 {A, C, A}가 되어 +1을 하여 3이 된다.
이어서 다음 열을 채우면 아래와 같다.

값을 채우다 보면 아래와 같은 규칙이 나오는 것을 알 수 있다.
- i 번째 문자와 j 번째 문자가 같다면, dp[i-1][j-1]의 LCS의 길이에 +1을 한다.
- i 번째 문자와 j 번째 문자가 다르면, dp[i-1][j]의 LCS의 길이(본인 기준 한 칸 왼쪽의 원소; 이전 행의 원소)와 dp[i][j-1]의 LCS의 길이(본인 기준 한 칸 위쪽의 원소; 이전 열의 원소)를 비교하여 큰 값을 선택하여 dp[i][j]에 채운다.
Code
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
char a [] = br.readLine().toCharArray();
char b [] = br.readLine().toCharArray();
int a1 = a.length;
int a2 = b.length;
int dp [][] = new int [a1+1][a2+1];
for (int i = 1; i <= a.length; i++) {
for (int j = 1; j <= b.length; j++) {
if (a[i-1] == b[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
} else {
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
bw.write(dp[a1][a2] + "");
bw.flush();
bw.close();
}
}'Algorithm PS > Baekjoon Online Judge' 카테고리의 다른 글
| [BOJ/백준] 11726 2×n 타일링 (S3) (0) | 2024.07.03 |
|---|---|
| [BOJ/백준] 1788 피보나치 수의 확장 (S3) (0) | 2024.07.03 |
| [BOJ/백준] 11053 가장 긴 증가하는 부분 수열 (S2) (0) | 2024.05.23 |
| [BOJ/백준] 9657 돌 게임 3 (S3) (0) | 2024.05.22 |
| [BOJ/백준] 1931 회의실 배정 (S1) (0) | 2024.05.17 |
